主旨
ラボラトリーオートメーションとは機械学習を用いて実験計画を効率化しようとする戦略である。例えば材料科学において目的の物性値を持った材料を少ない実験回数で合成しようとする場合に用いられる。今回のプロジェクトではトイプロブレムとして目標色を設定し、三つの色水(赤・青・黄)をどの割合で混ぜれば目標色に近づくかという最適化問題に取り組んだ。
手法
システム構成
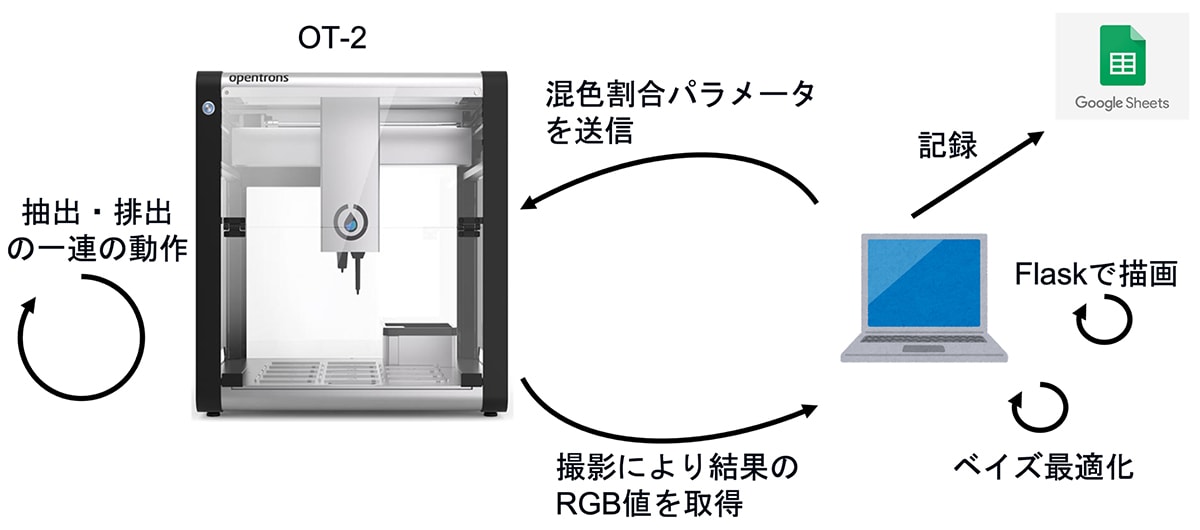
WebフレームワークであるFlaskでサーバーをたて、分注機と通信を行う。分注機はOT-2を用いた(https://opentrons.com/ot-2/)。
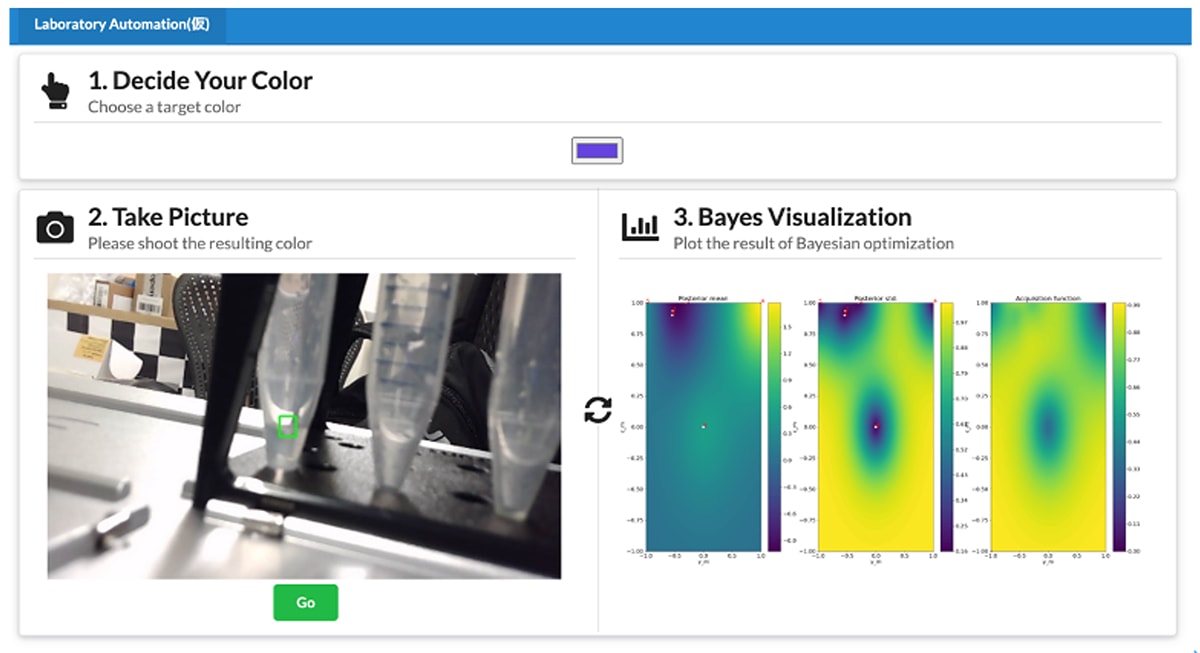
- 目標色を設定する。
- 分注機に色水の混色割合を送信する(初回は固定の初期値)。
- 混色が終了したら、カメラで撮影し、目標色との差分(損失)を計算する。
- ガウス過程を用いて、損失関数をモデル化し、表示する。獲得関数から次の混色割合を計算する。
- スプレッドシートに経過を記録する。
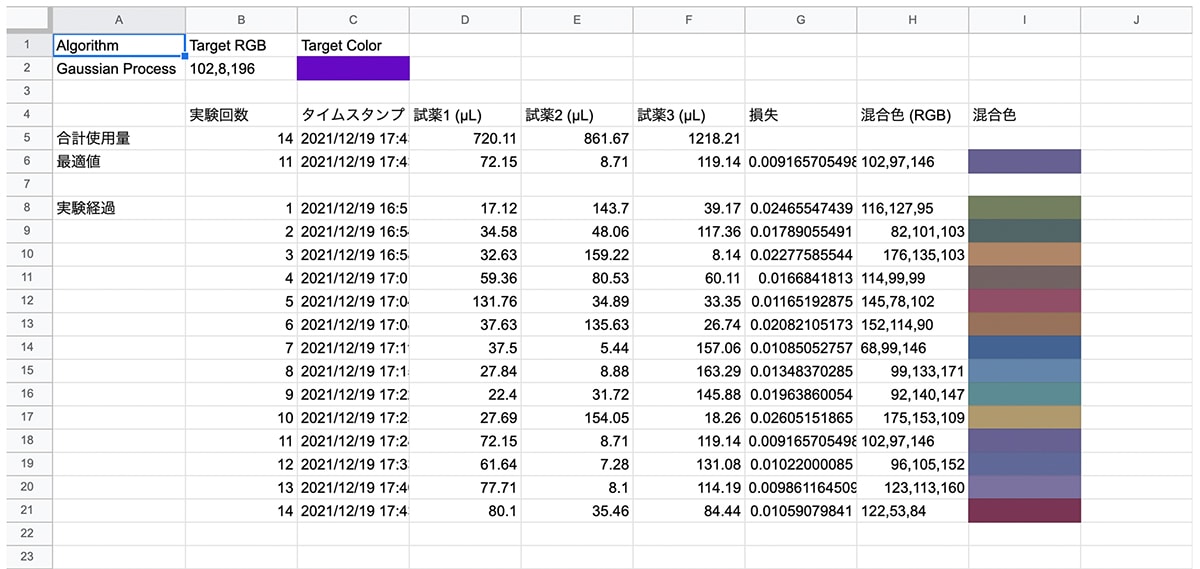
- 2〜5を繰り返す。
(補足)ガウス過程を用いたベイズ最適化の中身
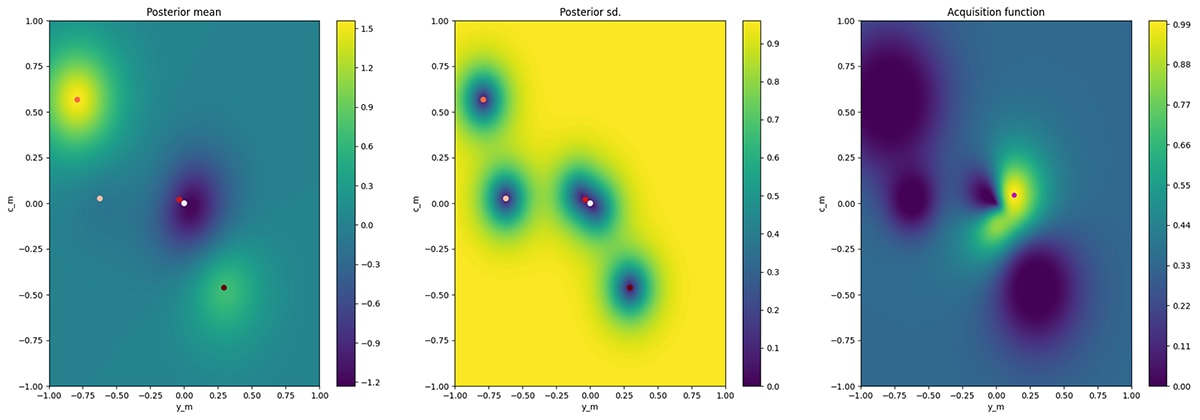
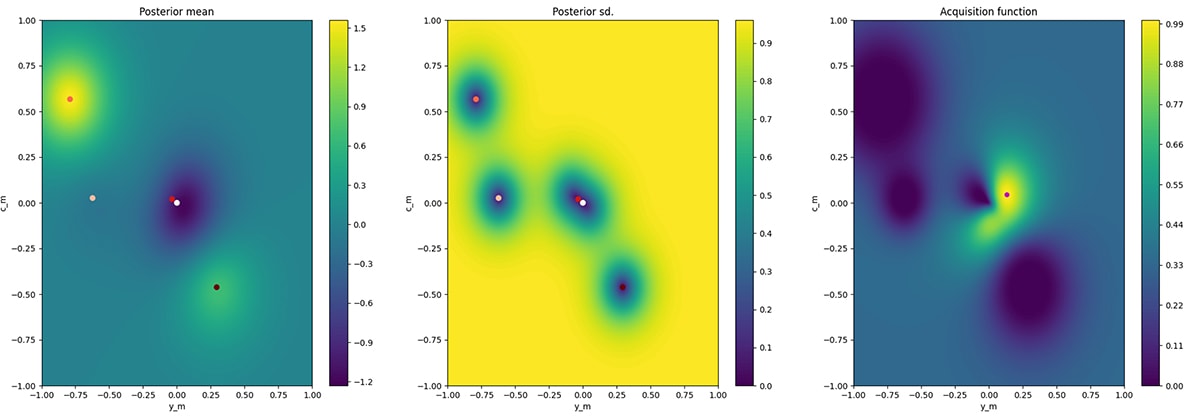
ガウス過程と呼ばれる技術を用いることで、過去の実験点から任意の点での損失を推定することができる。すなわち損失関数の形状がわかる(一番左の図の濃淡が損失の平均を表す、プロットは実験点、縦軸・横軸は混色割合)。ガウス過程を用いると推定した損失関数の値に自信を持っているかどうかを分散の観点から理解できる。実験点の近くは推定に自信があるので分散が小さく、離れれば離れるほど自信がなくなり分散が大きくなる(真ん中の図)。
最適化、すなわち損失を最小とする点の探索では、獲得関数と呼ばれる関数を計算する(一番右の図、赤い点が次の実験点)。獲得関数は過去の実験点から、最小となりそうな点を予測する関数である。
結果
探索5回目
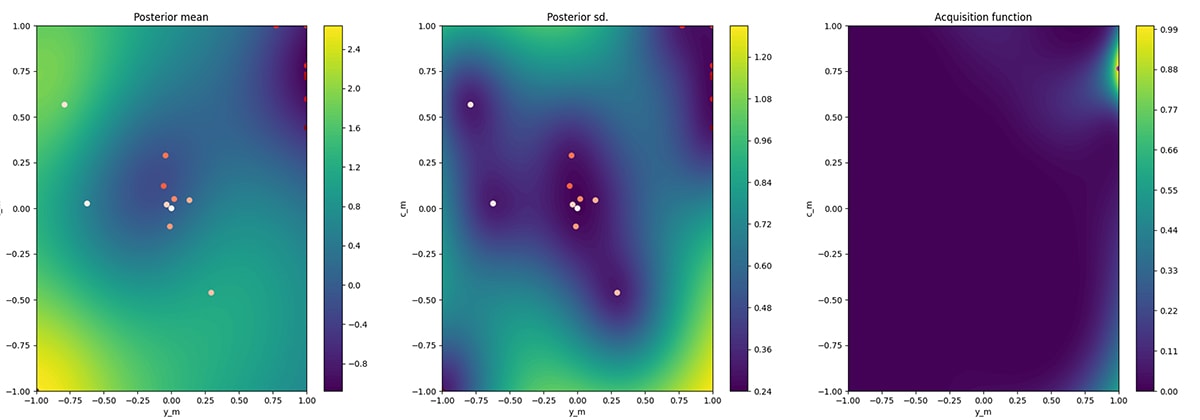
探索18回
考察
今回の実験はトイプロブレムであることから、人間が実験計画を立てて実験する場合と比べて、実験回数の大小を議論することはできない。 しかし、推定された損失関数の形状が妥当な形になっていることから、他の種類の実験でも同様に最適値に向かうことが期待できる。
展望
- 化学反応などを用いた高度な実験での最適化
応用を考え、トイプロブレムではない難度の高い実験でも最適化が行われ、人間が実験計画を考えるよりも少ない回数で正解に至れるか確認する必要がある。 - 実験の並列化
化学実験など一実験あたりの時間が長い場合に一つずつ実験を行うと効率が悪いため、複数の実験を並列に行い短縮を図る必要がある。
